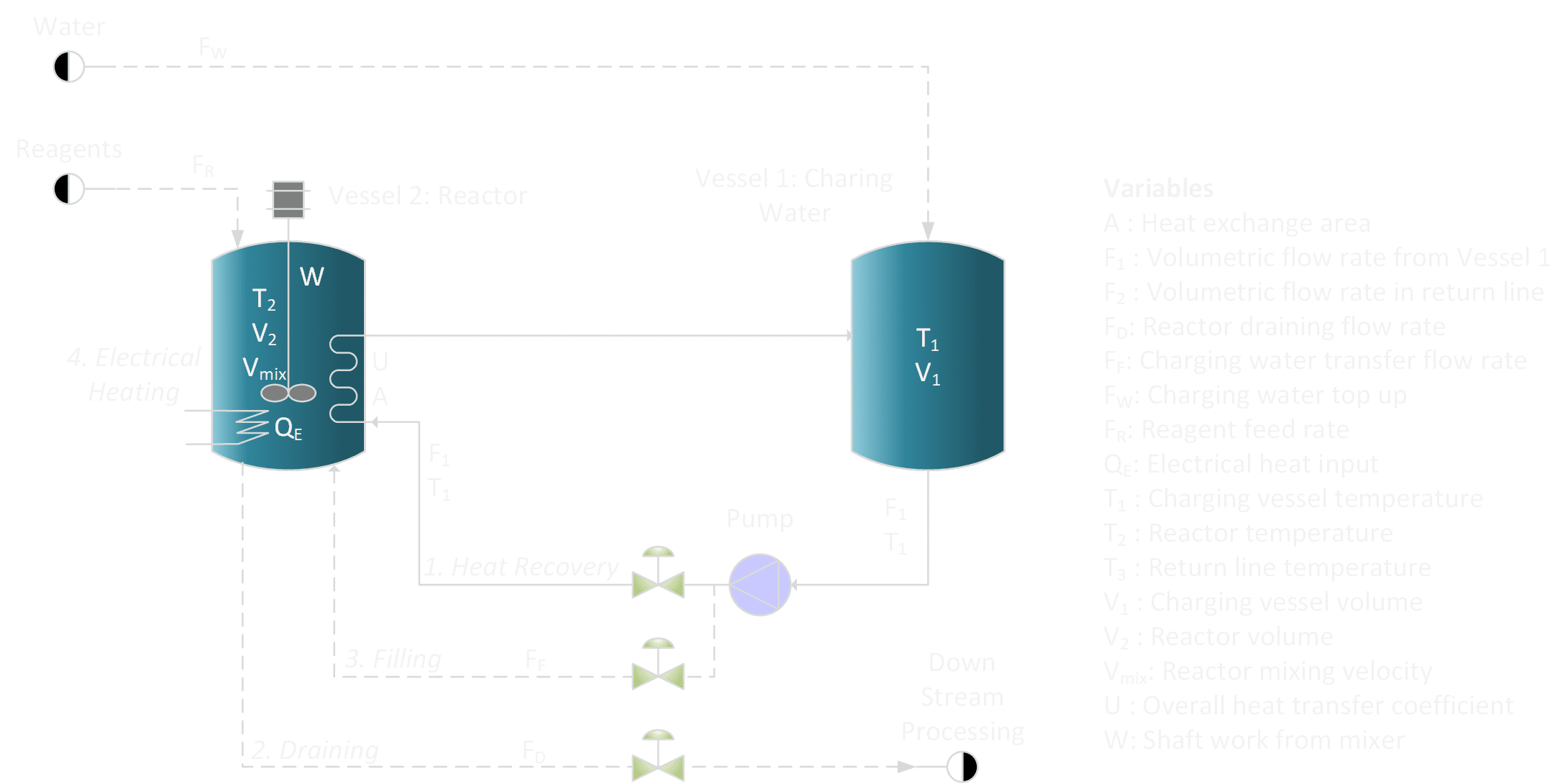
Modelling Heat Transfer to Optimise Energy Use: A Case Study
Introduction
Batch reactors find widespread application in diverse chemical processes, serving roles ranging from material blending and raw material reactions to fermentation and waste treatment, as exemplified here. A central operational hurdle faced by batch reactors is the considerable energy outlay required for elevating the reactor contents to the desired temperature. This can lead to notable energy expenditures and corresponding environmental consequences. To tackle this challenge, the integration of heat recovery systems is a common approach. These systems capture residual heat from the reactor, changeling it to preheat the incoming raw materials. Within this article, we delve into the initial modelling of a dynamic heat recovery setup for a batch reactor. This model holds the potential to significantly enhance energy efficiency and process economics.
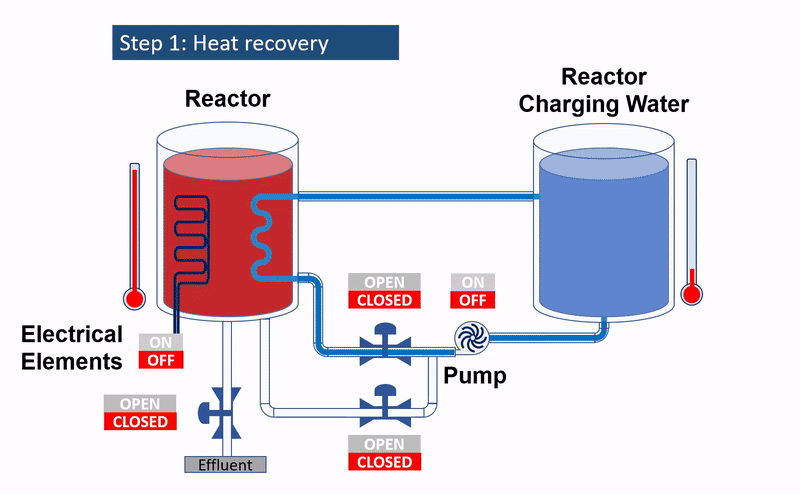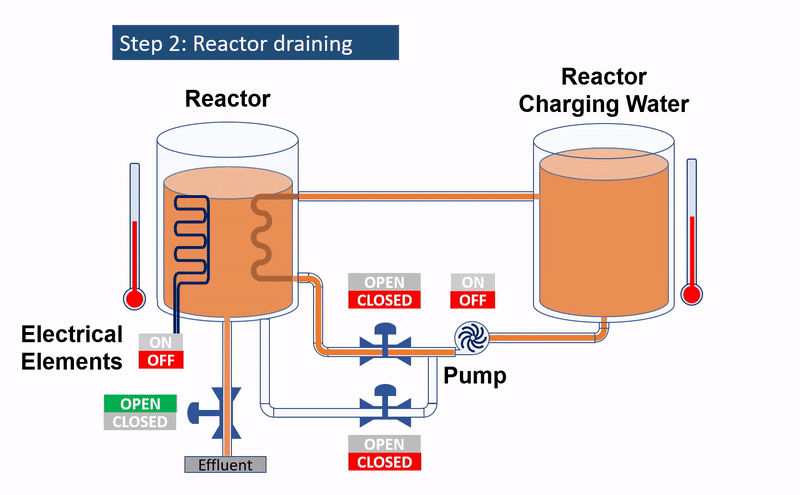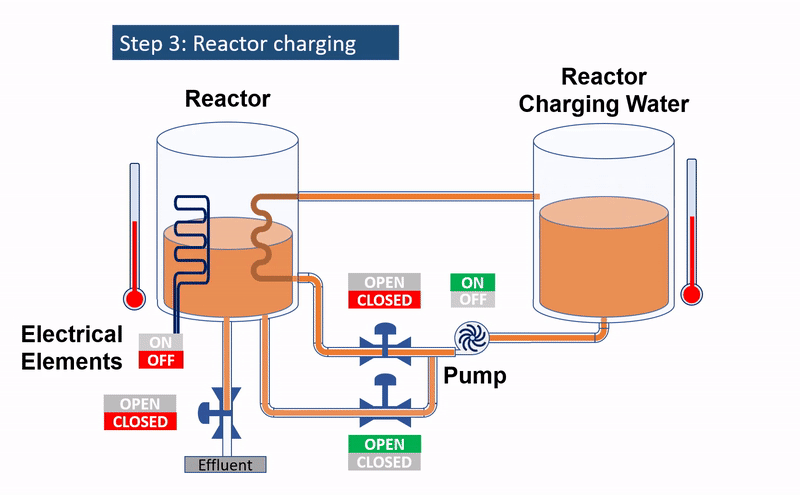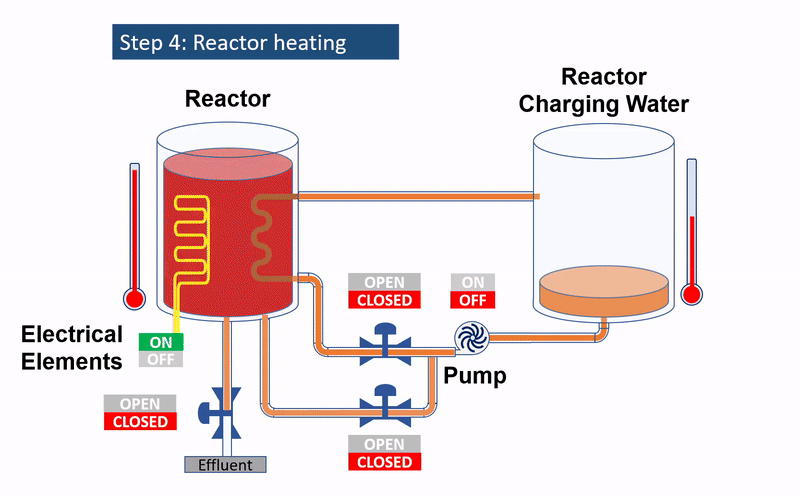
Defining the modelling problem
After the completion of the reaction, there is a critical need to cool down the hot reaction mixture before moving it to subsequent processes. A practical solution is to use the cold incoming charge, circulating it via a coil or jacket, integrated within or surrounding the reactor. This not only cools the hot reaction mixture but also heats up the incoming charge. Given the batch nature of this process, it is evident that we are navigating a transient heat recovery challenge that will later necessitate fine-tuning for optimal operation. To truly grasp the mechanics and achieve the desired outcome, it is essential to focus on specific variables: temperatures of the charging water, reactor, and the return line. Modelling these variables over time will not only provide insights into their dynamics but also guide us in establishing the most efficient operational strategy.
Formulating the Model
A mathematical model is derived to describe the heat recovery process. This is conducted using well known fundamental equations for mass and energy conservation. The figure shows a simplified diagram of the operation.
This mathematical modelling yields the following equation for describing the change in charging water temperature:
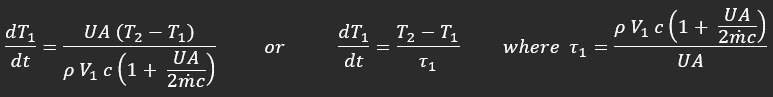
The following equation is derived to describe the change in reactor temperature:
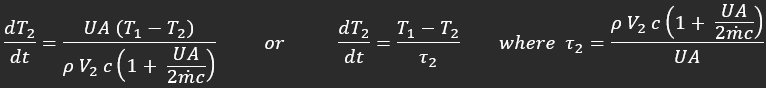
Solving the model
Once the modelling of the transient heat transfer system is well-established, a plethora of insightful observations can be extracted, guiding critical operational decisions. Firstly, the model can help identify the rate limiting factors in the heat transfer process. By simulating different operational conditions, we can predict how changes in variables like flow rate, mixing velocity, or initial temperatures can affect overall system performance. The model can be used to forecast the optimal time to initiate downstream processes, ensuring that the reaction mixture achieves the desired temperature, thus maximizing process efficiency. Another valuable insight is the identification of potential energy-saving opportunities. The model is also useful for testing the effects that changes to coil design will have directly on the required heat transfer time.
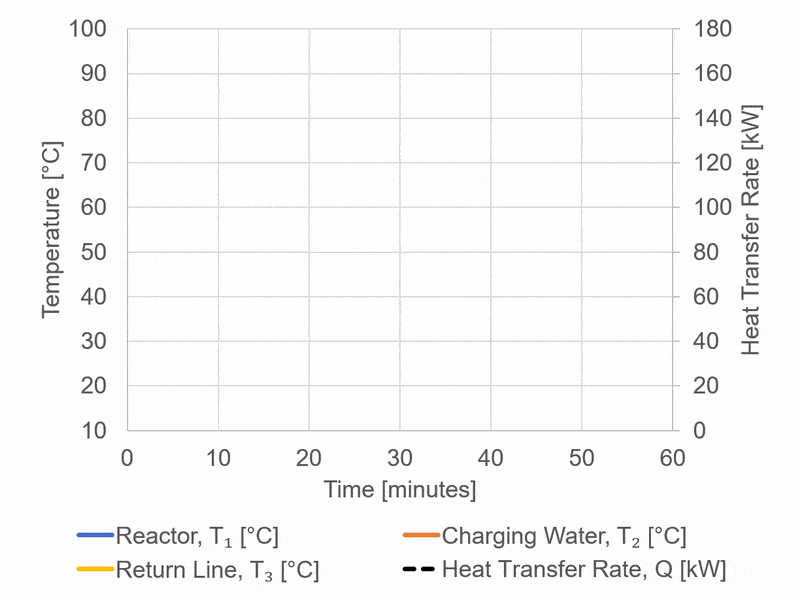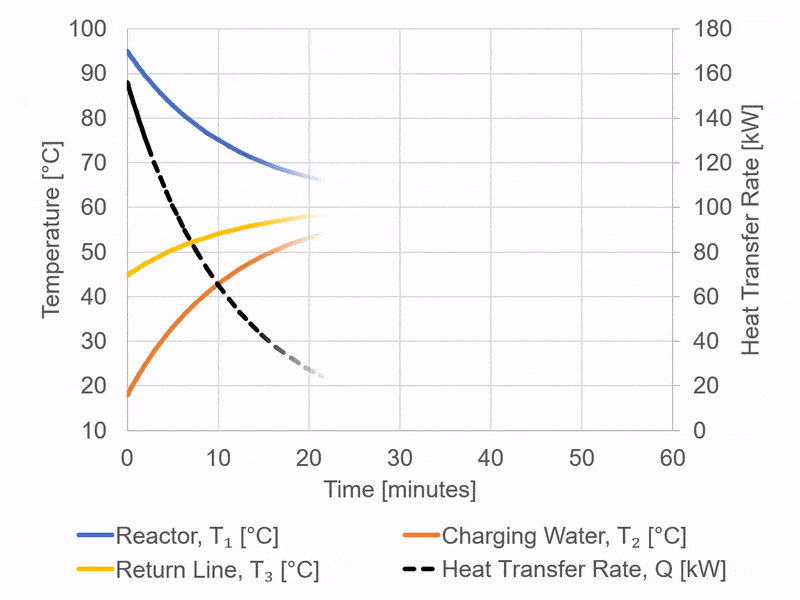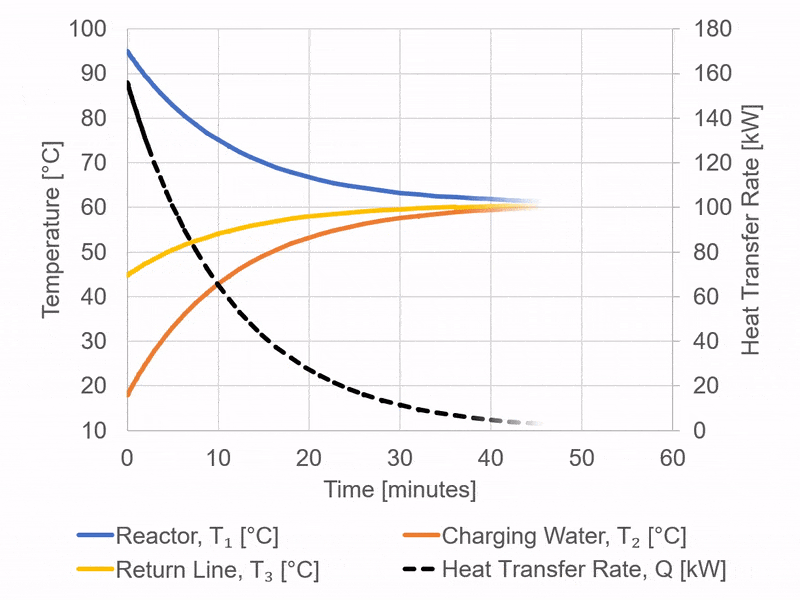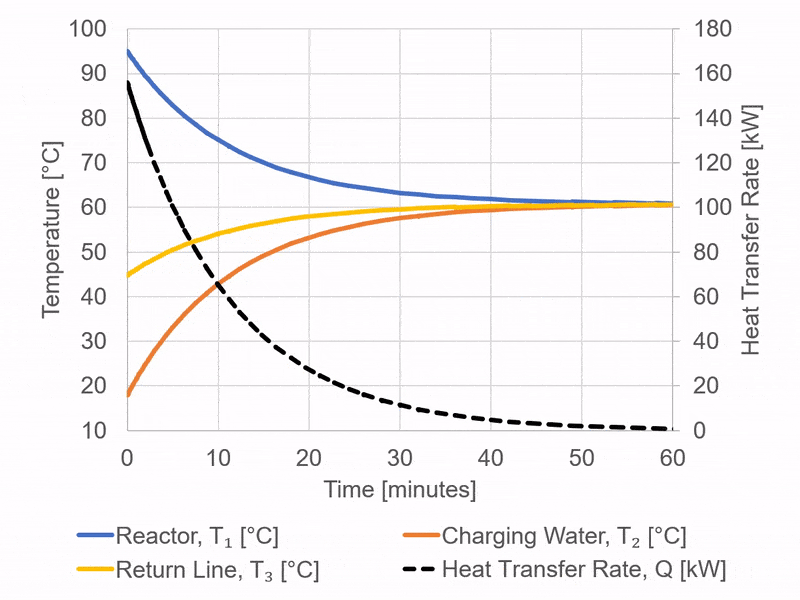
The figure shows model outputs for the temperature profiles achieved when circulating the cold charging water through the coils in the reactor.
The rapid convergence of the charging water and reactor temperatures is initially observed. This can be attributed to the large difference initially between the cold charging water and the hot contents of the reactor vessel. This temperature differential is the primary driving force for the heat transfer. As the difference in temperatures decrease, this driving for force decreases, and the pace of heat transfer decelerates.
How do we then decide at what point to halt the heat recovery process?
Prematurely terminating heat recovery leaves a notable amount of reusable heat unutilised; this would lead to escalating heating expenses for the succeeding cold batch. Conversely, an extended heat recovery phase would also extend the processing time per batch, consequently diminishing the reactor’s effective output. This scenario underscores the importance of operational optimization, which will be the focal point of an upcoming article.
In essence, with a well-defined transient heat transfer system model in place, engineers are equipped with a robust tool that can be used to not only optimize operational efficiency but also serves as a compass for continual process improvement and innovation.
Author: Willem Rossouw
Engineering Manager @ Macrotec
